Author: metatim

Categories
New

Things 114: Kern Test, Robot Bird, Social Graph, Too Soon To Say

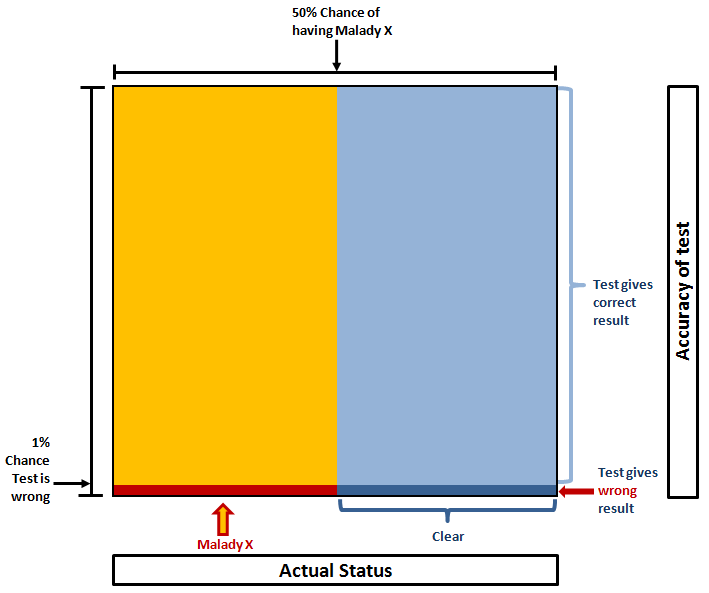
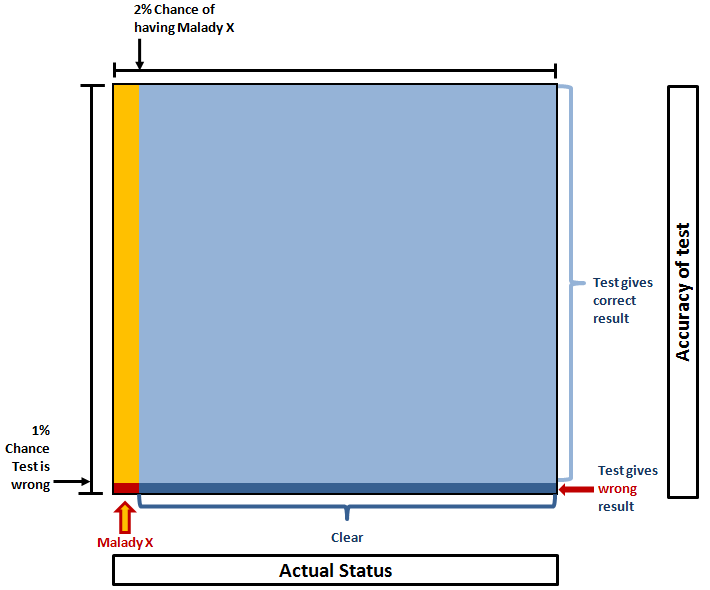
Puzzle
This week, try testing your ability to kern.

If you liked that, try the splines.

Video
It’s easy to get overexcited about human progress, when in the grand scheme of things we’re still pretty small fry. I would periodically remind myself of this by considering that for all our ingenuity, we still couldn’t make a robot the size of a bird that could fly like a bird. Thanks to the determined efforts of Festo, I’m going to need to come up with something else.

Link
I’ve seen this link crop up in a few places now, but for good reason – I think this is some really important stuff that we are collectively getting wrong on a large scale right now: “The Social Graph is Neither” by maciej.

Cutting large swathes of great text for concision, here’s my favourite part of the  argument:

[…] declaring relationships explicitly is a social act […] Social graph proponents seem uninterested in th[is] signaling problem. […] [and] how does cutting ties actually work socially? […]  In real life, all relationships fade naturally if you don’t maintain them, but right now social networks preserve ties in amber until we explicitly break them […] Can I unfollow my ex now, or is that going to make her think I’m still hung up on her?

[…] You might almost think that the whole scheme had been cooked up by a bunch of hyperintelligent but hopelessly socially naive people, and you would not be wrong.

However, after a lot of good stuff, it ends with something of a shrug:

It’s just a matter of waiting things out, and leaving ourselves enough freedom to find some interesting, organic, and human ways to bring our social lives online.

I’m not sure that’s quite the right way to put it. I don’t think it’s about bringing our social lives online. Its more about augmenting our social lives with online functionality that goes with the grain of human nature.

That said, leaving ourselves enough freedom is critical. Quite how we do that is a topic for another day.

Quote
In the early 1970’s, Richard Nixon asked Zhou Enlai what he thought of the French Revolution. Zhou notoriously responded:

It is too soon to say.

Which everyone thought was quite wonderfully representative of Chinese sagacity.

This year it emerged that the whole thing was a misunderstanding too delicious to invite correction, as Zhou thought Nixon was referring to the much more recent student riots in Paris.

But this doesn’t matter, because the misread quote still stands as a useful reminder that we should err towards taking a longer-term view when evaluating the benefits of things. On a similar note, Ben Hecht says:

Trying to determine what is going on in the world by reading newspapers is like trying to tell the time by watching the second hand of a clock.

Last Week’s Question
Last week I asked: when someone says “next Thursday” on a Monday, which Thursday do they mean?

Richard’s response was the same as mine – always clarify. However, where I was aware of two interpretations, he identified three [This part added thanks to Richard’s clarification – T.M. 25/11/11]:

I have come across three possible scenarios:

|

(a) this = first occurrence, next = second occurrence
(b) this = occurrence in the week you’re in, next = occurrence in the following week
(c) this = occurrence in the week you’re in, next = first occurrence

|

I don’t think anyone actually uses (a).
Personally I use (b).
I have met people who use (c).

|

To give some examples, on a Tuesday, referring to “This Monday”
and “Next Monday”.

|

(a) This Monday = 6 days times, Next Monday = 13 days time
(b) This Monday = -1 days time, Next Monday = 6 days time
(c) This Monday = -1 days time, Next Monday = 6 days time

|

I can’t think of anyone who would use (a).  (b) and (c) agree.

|

Another example, on a Tuesday, referring to “This Friday” and
“Next Friday”.

|

(a) This Friday = 3 days times, Next Friday = 10 days time
(b) This Friday = 3 days time, Next Friday = 10 days time
(c) This Friday = 3 days time, Next Friday = 3 days time

|

(a) is indistinguishable from (b), hence somewhere who is a (c)
might assume upon hearing (b) that their algorithm is actually
(a).  I would use (b).  I have met people who use (c).

However, I now wonder if this is paranoia – how divided are we really on this issue? Do the vast majority of people use one of these interpretations? My plan is to start to collect instances of people using this form of date referral, noting on which weekday it was said, and which day they were intending to refer to. I’ll report the results here when I have enough data, which may take a few years.

Categories
New

Things 113: Next Thursday, Learning to Cheat, Bullet Time

Question
When someone says “next Thursday” on a Monday, which Thursday do they mean?

Tim Link
Playing a trading/smuggling game at the recent Sandpit event at the National Maritime Museum, I did something more evil than I knew I was capable of. That got me thinking about the ethics of lying, what games taught me about that, and exactly how rules-based games can enable people to learn about breaking rules. The post is illustrated with playing cards, since I had some to hand.

Link
Two advantages of eBooks are that book size hardly matters, and you can easily link from one page to any other page. Now think about what this means for the choose-your-own-adventure genre. Jon Ingold found you could take a totally different approach, and produced a playable murder mystery that would be as tall as a house were it printed physically.

Quote
A nice way to remember confirmation bias:

Tolstoy: “The most difficult subjects can be explained to the most slow-witted man if he has not formed any idea of them already; but the simplest thing cannot be made clear to the most intelligent man if he is firmly persuaded that he knows already, without a shadow of doubt, what is laid before him.”

Picture
“Bullet time”

Categories
Old

Things 66: ChatRoulette piano, Tube Door Challenge, Free Will

(Originally sent March 2010, maybe)

Video
ChatRoulette is a fascinating site whose mission is simply to connect you to a random person to video chat with. This is just as good and bad an idea as it sounds. I don’t recommend visiting (particularly if you have a webcam active as it will attempt to throw you into a random encounter immediately) but I do recommend reading about it.

It turns out to be a great environment for improv performance as shown in this video (sound essential, 5’28” long but the first 40” gives you the idea):

I’m fascinated by the extent to which people respond silently – and contrast this with how we usually provide feedback to a musical performance. There’s some very interesting human-machine-human interface stuff going on here.

Link
Sometimes an aesthetic is a byproduct of technology – high contrast in over-reproduced 6”x10” glossy star photos, inconsistent speed in old black and white film, the depth and colour range in Polaroid photos, or the way 80s TV series look rubbish. Digital processing grants a whole new level of control over colour and the ability to choose from a vast range of possible palettes, but the result seems to be that everyone is doing the same thing. This is quite likely how films made in the last ten years will reveal their age when we look back on them ten years from now.

Quote
(via Tim Connor)

Marin Alsop: “Tradition is simply the last bad idea”

Picture
Free Will.

This weeks’ puzzle
Many years ago Nick challenged me to work out how to tell where the doors of a London Underground tube carriage would stop on the platform so that you could optimise where to stand to improve your odds of boarding first and so getting a seat. I came up with an answer that didn’t work terribly well but assumed that was what he had in mind (without ever confirming it). Only now after 5 months of catching 4 tube trains every workday have I realised a much better solution.

What do you think my first and second solutions were?

Last week’s puzzle
Why are calculator and phone keyboards laid out oppositely? There doesn’t seem to be a definitive answer, but there are a few very likely suspects.

The original decisions that led to 123 being at the bottom for calculators are unclear. Thomas suggests it’s a matter of “where your attention is coming from” – combined with Benford’s law I suspect this could be a key factor driving the layout of the first common mechanical number-entering devices, cash registers, and how devices evolved from there.

When it came to phone pads, it seems (remarkably for this kind of thing) that AT&T actually did some user testing and found the 3×3 grid with 123-at-the-top was the easiest for people to master. As letters were also a consideration in those days, putting ABC with 1 (and so on) made most intuitive sense, and would have looked pretty bizarre had 123 been at the bottom.

My preferred write-up of possible answers comes from The Straight Dope.

Various other attempts to answer this question are curated here.

Richard also points out the following (my summary of his words [my comments in square brackets]):

Handedness is a consideration for other aspects of the layout; in particular computer keyboard number keypads, which sit on the right-hand side, are supposed to be operated with the left hand [a revelation to me after years of feeling slightly odd using my little finger to press the return key], and an interesting challenge emerges when one keyboard is used for both data-entry/calculation and telephone operation, as with Skype today, or the over-prescient One-Per-Desk in 1984.

Categories
New

Things 112: Eyes, Guessing Cat, Amigara Fault

This week Things has a very slight Hallowe’en theme.

Puzzle
This is one where you should gather some people around the monitor and see who can do best: guess the cartoon (or CG) character from their eyes (mouse over the eyes to see the character outline that should tell you if you’re right).

And yes, it is pretty difficult – I only got 6, and I watch a lot of animation!

Video
Here’s a video that begs the question: is the cat playing the game, or just acting out of blind instinct?

http://www.youtube.com/watch?v=QrlTijuhVOA

To which the answer is to have a big argument about the definitions being used before concluding that you can’t tell.

Quote
In the wonderfully stylised animation The Secret of Kells, I heard the line “One beetle recognises another” and wondered if it was some kind of proverb. It turns out that it is, and actually – obviously – there are a whole bunch of Irish Proverbs, which in translated form become alternately profound, banal or hilarious, just as I imagine English proverbs must seem if you haven’t grown up with them. Here’s a list of them on Wikiquote, and here are a few of my favourites, for unstated reasons:

“Every beginning is weak.”

“Time is a good story teller.”

“A lamb becomes a sheep with distance…”

“The quiet are guilty”

Comic
The Enigma of Amigara Fault is a horror comic that impressed me with its unconventional approach. It’s 32 pages, and originally in Japanese so you have to read the panels right to left. But if you want a comic that will freak you out for Hallowe’en, it’s worth it. Unless you’re particularly claustrophobic, in which case you should probably steer clear of it entirely.

Answer – Malady X
In Things 111 I asked what the probability of having Malady X is if a randomly administered 99%-accurate test for it comes back positive. As Phil and Thomas noted, you can’t actually answer from this information alone: you also have to know what the probability of a random person actually having Malady X is. A lot of people don’t have an intuition for this fact. I’m going to attempt to explain ways to apprehend that hand-wavingly, mathematically, and visually.

Argument from hand waving and examples:
Imagine the probability of having Malady X is 0% – nobody has it. In this case, it’s certain that getting a positive result means you were simply in the 1% of cases where the test comes back incorrect.
Conversely if the probability of having it is 100% – everybody has it – then you must be in the 99% of cases where it is accurate. In this way, it’s clear the underlying probability influences the chances that the test is correct!

We might worry that these extremes somehow break the puzzle, so let’s imagine less extreme alternatives. Imagine 1,000 people are tested. If 50% (500) really have Malady X, on average we expect the test to come back positive for 99% of them (495) and also for 1% of the 500 that don’t have it (5). In this situation, 495 out of the 500 people for whom the test was positive actually have the disease – 99%.

Alternatively, if 1 person (or 0.1%) out of the 1,000 has the disease, they’re very likely to be correctly diagnosed, and we expect roughly 10 of the other 999 to get a positive result. In this case 1 out of 11 people with a positive result actually have Malady X – fewer than 10%. So clearly the underlying incidence level matters.

Argument from maths:
There are two probabilities at work: the chance the test is correct (99%) and the chance of anyone having Malady X (unknown – let’s call it X%). When you combine probabilities you multiply them, so for example the chance of anyone actually having Malady X AND getting a postive result is 99% times X%.

If someone gets a positive result and that’s all we know, we reason as follows:
A = Probability someone has Malady X and tests positive = X% times 99% times
B = Probability someone does not have Malady X but still tests positive = (100% – X%) times 1%
If you test positive, the chance you actually have it is C = A / (A+B). But if you haven’t studied probability carefully, I’m not sure you could infer this, which is why I like to come up with other ways of getting a feel for the correct answer.

Argument from visualisation:
Since there are two probabilities in question, and we combine probabilities by multiplying, this naturally suggests a visualisation where probability is represented by rectangular area (since area is calculated by multiplying height by breadth).

For example, if we imagine the actual incidence rate of Malady X is 50%, the picture would look like this (click for big):

If the test result is positive, you either have it and the result is correct (big yellow area) or you don’t have it but the test was incorrect (small dark blue area). The chance of you actually having Malady X is equal to the proportion of those combined areas that is yellow. In this case:
Yellow = 99% x 50% = 49.5%
Dark blue = 1% * 50% = 0.5%
Probability you have it = Proportion that is yellow = 49.5% / (49.5% + 0.5%) = 99%.

Alternatively if the incidence rate is, say, 2%, it looks like this:

Here we see the yellow and dark blue areas are very similar, so the chance of you being one or the other is much more even. In fact, it’s:
Yellow = 99% x 2% = 1.98%
Dark blue = 1% x 98% = 0.98%
Probability you have it = Proportion that is yellow = 1.98% / (1.98% + 0.98%) = 67% (ish).

As Peter Donnelly shows in this TED talk, this actually has some severe ramifications, because when the probability of the thing being tested for is extremely low, it becomes overwhelmingly likely that a positive result is false, but people intuitively feel that a 99% accurate test should be correct 99% of the time.

Thomas also noted:

If anyone is interested in playing around with the probabilities (even if you’re not familiar with the maths), I recommend GeNIe:
http://genie.sis.pitt.edu/
It lets you create networks of dependencies, set evidence and work out probabilities in problems just like these.

-Transmission finally ends