Tag: probability

Categories
New

Things July 2019: Bias, Co-operation, Location, Video Games

Extremely Generic Questions

In earlier iterations of Things I would often set readers a puzzle or ask a tricky question, with answers reviewed in the next edition. I’d like to start a new series of these that I’m calling Extremely Generic Questions: questions often asked, but not very specific or even necessarily well-defined. The puzzle is not only to try to find the best answer to a question, but also to understand why it is so often asked.

So, the first question: what is wrong with young people today?

Subconscious bias

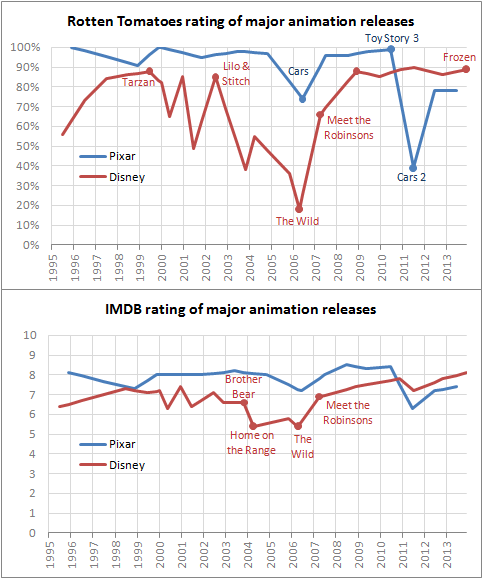
If you want to make optimal decisions, and also just be a decent person, I think subconscious bias is a very important factor to be aware of. Many people believe their judgement of aptitude is not influenced by gender (or any other unrelated characteristic), but data suggests this is not be the case.

Anecdotally but compellingly, there’s the email signature swap story, in which a male and female colleague swap their email signatures for a week and observe radical differences in how clients interact with them. Pleasingly, you can read the accounts of this from each side.

Auditions for an orchestra have the advantage that they can be conducted in a thoroughly meritocratic manner without ever actually seeing the candidates. It turns out that blind orchestra auditions improved women’s chances of success by 50%.

Similarly, scientific proposals for time using the Hubble Space telescope tried going partially blind; the results again showed women benefited from a more meritocratic process.

As I am sometimes involved with hiring people for work, I tried a version of this by making sure names were removed from CV’s before I reviewed them. Of course, I don’t have any large scale data to compare results, but the feeling of trying to assess a nameless CV was alarmingly transformative! It became very clear that as soon as I saw a name, I would start to construct a mental image based on (irrelevant) associations I had with people similarly named, and would then build on that image as I read the rest of the CV. Without a name as a starting point, the process of evaluation immediately felt like harder work, but also a lot more objective. Based on this and the above findings, I highly recommend it.

Thinking, Fast And Slow

After many years of seeing it recommended, I finally read Daniel Kahneman’s “Thinking, Fast and Slow”, which covers a lot of the biases I’ve been fascinated by for so long from essentially the very coal-face of that research.

I found it fascinating throughout and can see why so many recommended it, although I didn’t always agree with the interpretations. Given that I’m just some guy who studied maths/physics and read a few things, and the author is a Nobel prize winner with decades in the field, I have to recognise that my position on this is likely tenuous, but at least as far as maths go I feel I can comment.

Here’s my brief highlights.

Probability Problems
There is a strange and fuzzy line between not understanding what a question means, and not getting the answer right. I could ask people what 3 χ 4 is, and if they think it’s 12, that doesn’t mean they’re mysteriously misguided, it more likely means they just don’t know chi-notation*.  In many of the studies, participants were shown to give incorrect answers to statements involving probability, but one could just as well argue that participants didn’t really understand the statement and so were guessing. To be fair, the book goes on to show how phrasing probability questions differently (to my mind, more clearly) helps people reach more accurate results.

This is what I talked about in Things 122 on the topic of the Linda Problem / Conjunction Fallacy.

Forecasting and regression to the mean
I have to do quite a bit of forecasting at work, and I was surprised I had never come across this excellent rubric for anticipating a certain amount of regression to the mean.

Briefly: if you evaluate, say, fifty people on a task that involves some luck as well as skill, like accurately throwing something, then the people who did the very best (or the very worst) on their first attempt are unlikely to do as well (or badly) on a second attempt; their results were probably mostly flukes, and they will tend to ‘regress to the mean’.

If I am evaluating 12 different marketing campaigns and trying to forecast how well they do in future, the same kind of rule applies. The one that did very best was at least partially ‘lucky’, so will not necessarily be the best in future.

The rubric is as follows:
a) If the measure you want to predict has zero correlation with their future values (which you can figure out by viewing historical data), then you should predict that regardless of how they did, they will all perform averagely in future.

b) If the measure you want to predict perfectly correlates with the future, so whatever is the best now will be the best in future, then obviously you should predict that.

c) If the correlation between the present and the future is x%, then you should forecast any present deviation from average performance will decrease by (1-x)%!

That’s the terse version, you can read more about it here.

Evaluation of experiences
How much you liked or disliked an experience would intuitively be based on how long it was, and how much you were liking or disliking it at the time. Something that was unpleasant for 10 minutes should surely be ranked as worse than something that was unpleasant for only 5 minutes.

In practice, this isn’t how we evaluate things at all. We very highly weight our peak enjoyment (or discomfort), and how happy (or unhappy) we were at the very end of the experience, and a little bit the beginning; the absolute duration plays only a small part.

This probably means you should take fewer, shorter holidays, but it also depends on how you weight the importance of what Kahneman calls the “experiencing self” and the “remembering self”, which is quite a tricky philosophical problem.

Life is like an Iterated Prisoner’s Dilemma, except different

As a student I was very interested in the Prisoner’s Dilemma, and the iterated version, in which one must choose to Co-operate with (C) or Defect against (D) another player making the same choice, knowing that you will come out best (and they worst) if you D while they C, but you will both do terribly if you both choose D.

One critical element: you can’t communicate with the other player. In the iterated version, the choice of C and D is effectively the method by which you communicate.

Meanwhile in real life, most of the time, the thing most likely to help you is another human, and the thing most likely to do you harm is also another human, which means interacting with other humans is a pretty crucial business. In particular it’s good to be able to figure out – and influence – who is likely to co-operate (C) with you and who is likely to try to take advantage of (D) you.

I studied maths and physics as a student, but struggled to understand human behaviour. By studying subjects where exam answers were simply right or wrong, and doing quite well at those, I (and I suspect many others in the same situation) thought that I must be quite clever, and the reason I can’t understand human behaviour is because other people are just acting irrationally.

Now, it is true that people act irrationally a lot of the time (see the last Things), but that also includes me, and a lot of the things I couldn’t understand eventually made more sense when I realised that life was like an iterated Prisoner’s Dilemma, except that rounds aren’t discrete or simultaneous and there are multiple and varying pay-off matrices in play all the time.

For example, I noticed people asked “How are you?” but didn’t actually want to know, which seemed irrational. This was laid bare for me in a dentist’s waiting room when one elderly person entered and recognised another, and the following exchange took place:

A: Oh, hello there! How are you?
B: I’m fine, how are you?
A: I’m fine thanks. So [short pause] how are you then?
B: Well, I’ve been having this awful pain in my side, so I went to the doctor last week …

Similarly, as a marketing grad I was sent out with a cameraman to stop people on the street and get their opinions on climate change for a vox pop montage. I would walk up to people and ask them right away, and nobody stopped to answer. The cameraman, who had done this before, told me I should ask them how they were first. This seemed ridiculous, as a person approaching you with a microphone and film camera obviously doesn’t care how you are, they just want to film you saying something. But I tried asking anyway, and suddenly just about everyone was then happy to give their opinion on climate change for the camera.

I realised the whole “How are you” bit is like a tiny move in an iterated Prisoner’s Dilemma in which you are really communicating “I will co-operate with you”, and the other person can demonstrate a reciprocal intention by asking you the same thing back. This then sets the scene for further and deeper co-operation.

Moves aren’t just made in speech either. I thought buttoned shirts were ridiculous in comparison with t-shirts: uncomfortable, more time-consuming to put on and remove, and harder to clean. Why would anyone choose to wear one? But it turns out clothing is a widely understood opening move in our co-operation dialogues. We learn that we can estimate by someone’s clothes how likely they are to co-operate with or benefit us in certain ways; uniforms do this in an overt way, but even a slight deviation from your company’s dress code sends a signal.

Cat and girl covered this, of course.

More generally, these kinds of behaviours make a society cohesive – by doing what everyone else does, you tacitly signal that you are a good co-operator in your society. At the same time it can make society conservative, as anyone deviating from locally normal behaviour (even for rational reasons) might be read as less co-operative, and so they will encounter more friction.

Location Encoding

What3Words (W3W) assigns each 3m x 3m square on Earth a three word designation (e.g. Each.Useful.Shark). This makes it fantastic for real-world treasure hunts, so long as the participants can use the mobile app, and I’ve made a couple of events that leveraged it to (I thought) rather fun effect.

However, Richard brought to my attention that among people interested in the general problem of addressing, W3W is viewed very negatively. Why is that?

Reading up on the subject (this post was particularly useful), it seems like W3W lacks some attributes a truly general Location Encoding system should really have. But what really annoys people who understand this area well is that W3W tends to put out PR that claims to be strong in the areas it is weak. In brief:

  • W3W is a private company (probably hoping to be acquired by another one). Location/address is something that works best when it’s a standard, and having a private company own a standard leads to conflicts of interest. (See the Microsoft ‘Embrace, Extend, and Extinguish’ strategy for an example of how private companies fight public standards).
  • W3W is not a good solution for emergency situations (calling an ambulance to your location; calling a Fire Engine to a location you see on fire).
  • W3W is not error tolerant and has no hierarchy (e.g. one mis-spelt/mis-remembered character has very little chance of being corrected, in contrast with traditional addresses, where post accurately addressed apart from saying “Brighton” instead of “Hove” still successfully gets to Hove with the word Brighton angrily crossed out and corrected).

Still, I do think W3W has some value, and it would be unreasonable to discard it entirely because it can’t do everything – indeed, no address system can meet all the requirements we might ask of it.

Google Maps’ location-sharing functionality covers many options, and has the benefit of being already available in many people’s pockets, but I recently had a situation where both intuitive addressing and Google failed: meeting at the “Joe’s Café in Soho” does not specify a unique location, and the inaccuracy of GPS meant a shared Google location didn’t resolve the matter either. W3W is actually pretty excellent for this sort of spontaneous meeting. All things considered though, the best thing about it really does seem to be the opportunities for Treasure Hunts.

Video Games

I’ve played some games since the last Things, some of which I recommend, and some of which I don’t!

Baba Is You (Steam, Humble store, itch.io, Switch)

The mostly instantly-gettable trailer seems to be in this tweet:

For Things readers partial to self-referentiality and all things meta (and I know there are a bunch of you), this is certainly worth a look. As the above video shows, the game is played by pushing things around, including words that define the rules of the game.

In practice it’s even more mind-boggling than I expected, but not actually as much fun as I had hoped.

Celeste (Steam, itch.io, Switch, PS4, Xbox One, Pico-8 prototype)
If you want a platform game with puzzle elements and enjoy dying repeatedly while you slowly get better at doing difficult things, this is extremely the thing for you. The soundtrack is quite lovely too.

My save file, 44 hours, 10,000+ deaths, is a review in itself (implicit spoilers split-by-level version is here):

Lovers in a Dangerous Space Time (Steam, Switch, PS4, Xbox One)
Looks exactly like what it is: a rather nice local co-op shooter in which you and some friends control characters running around a ship manning the helm/gun/shield/panic-button and rescuing animals in space.

Thomas Was Alone (Direct for Mac or PC, iOS, Android, Steam)
A kind of “self-aware” puzzle-platformer that everyone was going on about a few years ago; I finally tried it and found it dull and not at all as funny as it seemed to think it was, with frustratingly vague platforming physics.

The Legend of Zelda: Breath of the Wild (Switch and Wii U only)
An open world epic about saving the world which I tried – and failed – to enjoy for about 12 hours before giving up. Almost everything about it felt like a chore and I couldn’t understand how it gained such universal acclaim.

After a weirdly long time adventuring in my underwear, I finally found someone who would sell me clothes.

To pick one example, a complaint I had heard from some was that weapons could only be used a certain amount of time before they fell apart and had to be replaced. I thought this was just misguided resentment of a feature clearly designed to add strategy to battles, but then I spent the first hour of the game picking up and discarding 37 differently ineffectual sticks (you can only hold a few at a time) and fought about 5 monsters. It felt like I spent substantially more time managing my ineffectual stick inventory than having battles, and so the whole weapons feature then felt like busywork.

Loading screen tip: read loading screen tips. By definition, this is useful to nobody.

Perhaps the worst part is I still feel like I “should” give it more of a chance, or at least get more entertainment for my money, when rationally I know there must be more games out there like Celeste which were an order of magnitude more fun for a fraction of the price.

Horizon Zero Dawn (PS4 only)
Snakes on a Plane is a great title for a film because it perfectly sells the premise. Horizon Zero Dawn is a terrible name in that regard, but the promotional art sells the premise perfectly:

Tribal humans hunting robot dinosaurs! Which immediately looks like something I want to try, and also very quickly raises the question of just how such a scenario could even come about. It turns out the game is exactly about those two things: hunting robot dinosaurs while figuring out how this happened!

It certainly stands on the shoulders of giants in terms of the use of ‘Open World’ game conventions, but it adds a few interesting ideas and does just about everything you would hope to extremely well.

*I made up “chi-notation”, because I couldn’t think of a clearer example, it seemed funny, and illustrates the point just as well.

– Transmission finally ends

Categories
New

Things 131: Frozen is objectively great, Internet decay and hamsters, Shower danger

Data-based movie recommendation
In 2010, with the release of Disney’s The Princess and the Frog, I looked back at the historic trends to try to understand where Disney went wrong in the 00’s. The Princess and the Frog (and Bolt before it) were successful in terms of IMDB and Rotten Tomatoes ratings, but less so in terms of revenue.

I concluded that Disney had to somehow maintain this level of quality in order to build back their reputation. With Tangled, Wreck-it-Ralph, and most recently Frozen, that’s exactly what they’ve done. In fact, since 2011, they’ve consistently outperformed Pixar (despite owning them):

Frozen currently enjoys the highest IMDB rating Disney have received since The Lion King, although due to self-selection it will be somewhat overstated in these initial weeks after its release.

On a more personal note, I’ve now seen Frozen twice, and highly recommend it – do be advised that it is a full-on musical, but co-composed by one of the people behind The Book of Mormon, so there’s a lot to enjoy even if that wouldn’t usually be your cup of tea. It’s also highly notable for having two female leads with real agency (I’m looking at you, Brave, with your arbitrary plot-advancing Will O’ the Wisps).

Video –Automated Automata Architecture
Continuing the Disney-is-actually-pretty-good-now theme, here Disney research demonstrate how they can generate the gearing required to closely recreate an arbitrary cyclical movement, then 3D-print the result to make the automaton. I particularly like the cyber tiger at 3’30”:

(via The Kid Should See This)

Tumblr – Video games with modified objectives
“No wrong way to play” collects examples of people playing video games in ways not intended by the designers. I approve of this.

Tim Link – Learning to Cheat, part 3
Two years ago I surprised myself by betraying someone pretty meanly in a public game. I began a series of blog posts post-rationalising the whole thing within a game-design framework, and after a guilty two-year gap I finally posted my full confession and/or excuse.

Internet decay
If you’ve ever navigated early entries of Things on the blog, you might have seen some dead links, and some links which went dead and got fixed, and some which died again, as I periodically go back and attempt to fight digital entropy.

Based on this insignificant sample, it seems like the half-life for links on the internet is 5-10 years, and considerably less for YouTube videos. This is pretty distressing as laziness/convenience drives us to rely on the internet for files we’re interested in – after all, your options are essentially a) saving a lolcat in downloads>pictures>cats, renaming the file so you can easily find it, and maintaining off-site backups of your data to hedge against hardware failure, or b) just image search “I have a cat and I’m not afraid to use it” from any device, which is a lot more appealing. (Naturally I still choose option a).

There’s a few good links on the subject here, including the compelling quote:

“People are coming to the realization that if nobody saves the Internet, their work will just be gone.” – Alexis Rossi, Internet Archive

Hamster fighting machine / response
Here’s an example of why it’s important to hold onto things on the internet. In 2005, Jarred Purrington made the Hamster Fighting Machine comic/poster (which you can see here or here but not on the original link because it’s dead)

In 2010, Dale Beran (writer of previously-Thinged webcomic/cogent nightmare “A lesson is learned but the damage is irreversible”) posted a lovely response.

Answer – 100 Chalices
Last time I asked if you should choose a chalice with 50/50 odds of being poisoned over one random chalice out of 100 which 100 fiends have each independently and randomly poisoned one of.

Restated, this is asking if you would prefer one-hundred 1-in-100 chances of death vs a single ½ chance. Richard correctly reasoned that the average amount of poison-per-chalice is double in the 100-chalice room, and some degree of bunching in the distribution (i.e. some chalices getting poisoned multiple times) didn’t seem likely to offset it, so the 50/50 chance is probably the best bet.

For any of you not familiar with the probability behind this sort of thing, here’s a quick summary. In the 100-chalice case, calculating all the ways a chalice could get poisoned is very difficult, but calculating the probability of it never getting poisoned is much easier as there’s only one way that can happen. The odds of avoiding poison any one time are 99/100, and this has to be repeated 100 times. So:

Odds of avoiding poisoning = 99/100 x 99/100 x … x 99/100 = (99/100)^100 = 37%. Clearly not as good as the 50% chance in the two-chalice room.

As a post-script, if you’re interested, the expected ‘bunching’ of poisonings would look a bit like this:

This is also a very important concept when evaluating risks in your own life for things that you repeat. For example, I noticed that I tended to step out of the shower in a needlessly risky way, with a risk of slipping (and getting seriously hurt) of perhaps 1-in-a-thousand. That seems tolerable, until you consider that if I showered once a day for 2 years, my odds of avoiding such a fate would be (999/1000)^730 = 48%, in other words I’d be more likely to have at least one such accident than not! So, watch out for that.

Answer – Kickstarter videos
I’ve spoken to a few people about the fact that Kickstarter videos always make me feel less motivated to put my money in. The underlying reason seems to be that a Kickstarter page typically does a great job of selling the product/reward, but the video often ends up being more about selling the people behind it (as being worthy, or in need of your money). Before the video I don’t even think about that; after the video, that’s just another reason to say no.

-Transmission finally ends

Categories
New

Things 112: Eyes, Guessing Cat, Amigara Fault

This week Things has a very slight Hallowe’en theme.

Puzzle
This is one where you should gather some people around the monitor and see who can do best: guess the cartoon (or CG) character from their eyes (mouse over the eyes to see the character outline that should tell you if you’re right).

And yes, it is pretty difficult – I only got 6, and I watch a lot of animation!

Video
Here’s a video that begs the question: is the cat playing the game, or just acting out of blind instinct?

http://www.youtube.com/watch?v=QrlTijuhVOA

To which the answer is to have a big argument about the definitions being used before concluding that you can’t tell.

Quote
In the wonderfully stylised animation The Secret of Kells, I heard the line “One beetle recognises another” and wondered if it was some kind of proverb. It turns out that it is, and actually – obviously – there are a whole bunch of Irish Proverbs, which in translated form become alternately profound, banal or hilarious, just as I imagine English proverbs must seem if you haven’t grown up with them. Here’s a list of them on Wikiquote, and here are a few of my favourites, for unstated reasons:

“Every beginning is weak.”

“Time is a good story teller.”

“A lamb becomes a sheep with distance…”

“The quiet are guilty”

Comic
The Enigma of Amigara Fault is a horror comic that impressed me with its unconventional approach. It’s 32 pages, and originally in Japanese so you have to read the panels right to left. But if you want a comic that will freak you out for Hallowe’en, it’s worth it. Unless you’re particularly claustrophobic, in which case you should probably steer clear of it entirely.

Answer – Malady X
In Things 111 I asked what the probability of having Malady X is if a randomly administered 99%-accurate test for it comes back positive. As Phil and Thomas noted, you can’t actually answer from this information alone: you also have to know what the probability of a random person actually having Malady X is. A lot of people don’t have an intuition for this fact. I’m going to attempt to explain ways to apprehend that hand-wavingly, mathematically, and visually.

Argument from hand waving and examples:
Imagine the probability of having Malady X is 0% – nobody has it. In this case, it’s certain that getting a positive result means you were simply in the 1% of cases where the test comes back incorrect.
Conversely if the probability of having it is 100% – everybody has it – then you must be in the 99% of cases where it is accurate. In this way, it’s clear the underlying probability influences the chances that the test is correct!

We might worry that these extremes somehow break the puzzle, so let’s imagine less extreme alternatives. Imagine 1,000 people are tested. If 50% (500) really have Malady X, on average we expect the test to come back positive for 99% of them (495) and also for 1% of the 500 that don’t have it (5). In this situation, 495 out of the 500 people for whom the test was positive actually have the disease – 99%.

Alternatively, if 1 person (or 0.1%) out of the 1,000 has the disease, they’re very likely to be correctly diagnosed, and we expect roughly 10 of the other 999 to get a positive result. In this case 1 out of 11 people with a positive result actually have Malady X – fewer than 10%. So clearly the underlying incidence level matters.

Argument from maths:
There are two probabilities at work: the chance the test is correct (99%) and the chance of anyone having Malady X (unknown – let’s call it X%). When you combine probabilities you multiply them, so for example the chance of anyone actually having Malady X AND getting a postive result is 99% times X%.

If someone gets a positive result and that’s all we know, we reason as follows:
A = Probability someone has Malady X and tests positive = X% times 99% times
B = Probability someone does not have Malady X but still tests positive = (100% – X%) times 1%
If you test positive, the chance you actually have it is C = A / (A+B). But if you haven’t studied probability carefully, I’m not sure you could infer this, which is why I like to come up with other ways of getting a feel for the correct answer.

Argument from visualisation:
Since there are two probabilities in question, and we combine probabilities by multiplying, this naturally suggests a visualisation where probability is represented by rectangular area (since area is calculated by multiplying height by breadth).

For example, if we imagine the actual incidence rate of Malady X is 50%, the picture would look like this (click for big):

If the test result is positive, you either have it and the result is correct (big yellow area) or you don’t have it but the test was incorrect (small dark blue area). The chance of you actually having Malady X is equal to the proportion of those combined areas that is yellow. In this case:
Yellow = 99% x 50% = 49.5%
Dark blue = 1% * 50% = 0.5%
Probability you have it = Proportion that is yellow = 49.5% / (49.5% + 0.5%) = 99%.

Alternatively if the incidence rate is, say, 2%, it looks like this:

Here we see the yellow and dark blue areas are very similar, so the chance of you being one or the other is much more even. In fact, it’s:
Yellow = 99% x 2% = 1.98%
Dark blue = 1% x 98% = 0.98%
Probability you have it = Proportion that is yellow = 1.98% / (1.98% + 0.98%) = 67% (ish).

As Peter Donnelly shows in this TED talk, this actually has some severe ramifications, because when the probability of the thing being tested for is extremely low, it becomes overwhelmingly likely that a positive result is false, but people intuitively feel that a 99% accurate test should be correct 99% of the time.

Thomas also noted:

If anyone is interested in playing around with the probabilities (even if you’re not familiar with the maths), I recommend GeNIe:
http://genie.sis.pitt.edu/
It lets you create networks of dependencies, set evidence and work out probabilities in problems just like these.

-Transmission finally ends

Categories
New

Things 111: Malady X, Stretching Cat, 3 Panels

Question
(Thanks to Simon for reminding me of this important probability lesson!)

At random, you are tested for Malady X. Alarmingly (particularly given that you don’t even know what Malady X is) the test comes back positive. But you know these tests are not always perfect – there’s a chance that it’s wrong, and you don’t really have Malady X at all. So you ask how accurate the test is. You are told that if someone really does have Malady X, there’s a 99% chance the test will come back positive; for someone that doesn’t have it, there is a 99% chance the test will come back negative.

What is the probability that you actually have Malady X?

Animated Gif
Here is the best animated gif of a cat I have seen in a long time:

Link
(via Silv3r): A huge and (I think?) growing collection of street fliers that play with the form, some okay and others quite, quite brilliant, can be found here (browse the other pages if you like what you see).

Picture
I am proud to be able to say that I know James White, the author of this perfect 3-panel comic, personally.

Answer
Last time I asked about what people really mean when they claim “change is accelerating”.

The most direct and plausible answer came from John B, who suggested that the scope of human knowledge is the thing that is really growing, and the subjective change we experience is what arises from these discoveries. While it’s only a proxy, one way to measure this is to track how many patents are granted over time, and on a logarithmic scale this does look kind of linear (indicating acceleration).

Bex has an alternative view. The perception of change seems to generally accelerate with age (which in itself is already enough to explain why people claim this all the time). The population of the UK (at least) is ageing. Therefore, the speed-of-change will be reported to be, on average, faster over time. Sneaky!

As the Wikipedia article on the subject currently notes, another confounding factor could be the growth of the human race itself. For example, if a fixed proportion of humans files patents, exponential growth in human race will directly lead to exponential growth in patents filed.

In any field, taking any trend and extrapolating it arbitrarily far into the future is generally unwise. If we don’t know exactly what we’re measuring, and we don’t understand the factors governing the change, even less so. Given the potential disruptions of the technology we’re seeing already, if anything it seems just as likely to me that sudden power imbalances become more likely, which could lead to large swathes of humanity being wiped out, or global human society turning into a dead-end all-powerful dictatorship with no desire to change the status quo.