Video
The effect of music on the brain is a very interesting thing that varies tremendously by individual. Last year I discovered a track that has an incredibly powerful mood-altering effect on me: Olympians, by a band with a potentially offensive name. It took a couple of initial slightly bemused listens before it properly seeped into my brain, but now as soon as I hear this track, I feel unbelievably positive, and become filled with an absurd confidence.
Unfortunately I suspect the fact that this track is so resonant for me also suggests that it’s very specific, and it will seem really quite boring to most others. But I find it so amazing I just have to share it anyway. So first, here’s a short version with a video to slightly entertain you while you wonder what on earth I’m going on about:
And if you are so inclined, here’s the full length version:
Tim Link
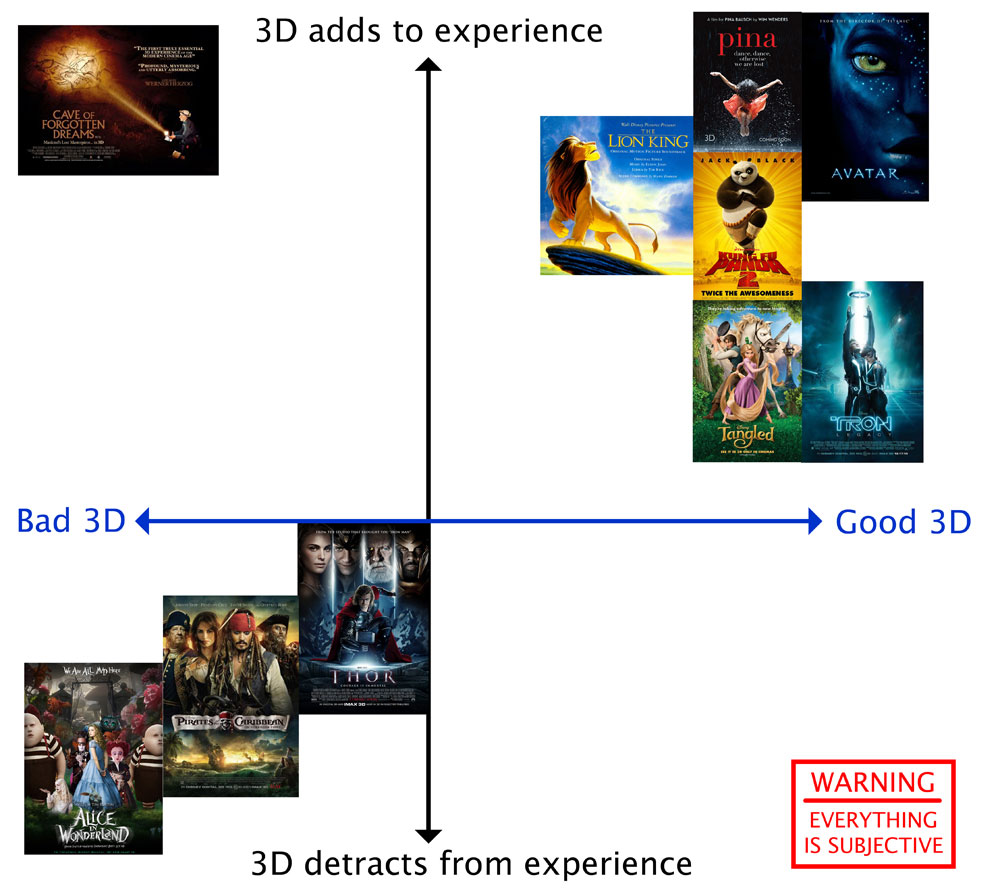
I saw The Lion King in 3D at Edinburgh International Film Festival, and reviewed it here. The short version of my review would essentially be this:
Quote special: Misleading Impressions
Thanks to Last.fm recommendations I discovered Brian Transeau (BT)’s album This Binary Universe, which turns out to be a bit different to his other albums. As I listened to his back-catalogue I thought I detected an incredible sense of optimisim and positivity. When I later found Brian Transeau was on Twitter, I found this impression was entirely correct. Sample tweet:
5am and time for our first ever sunrise, father daughter bike ride. Today is already #WIN Good Morning!
My favourite musician is probably Jon Hopkins who I now listen to instead of any other Chill Out music since for me he somehow trumps pretty much the entire genre. He is behind some of the most relaxing and beautiful tracks I know, so I was curious to see what he was like on Twitter. The answer: actually a bit different. Brilliantly, this was the first Tweet of his that I read:
I wish one of James May’s Big Ideas was to FUCK OFF
Finally, moving away from music, I referenced Mitch Hedberg’s famous escalator line in my Lion King 3D review:
An escalator can never break – it can only become stairs.
Realising I was unfamiliar with his work, I ended up reading through his Wikiquote page, and found much to like, such as:
My belt holds up my pants and my pants have belt loops that hold up the belt. What the fuck’s really goin on down there? Who is the real hero?
and:
When you go to a restaurant on the weekends and it’s busy they start a waiting list. They start calling out names, they say “Dufresne, party of two. Dufresne, party of two.” And if no one answers they’ll say their name again. “Dufresne, party of two, Dufresne, party of two.” But then if no one answers they’ll just go right on to the next name. “Bush, party of three.” Yeah, what happened to the Dufresnes? No one seems to give a shit. Who can eat at a time like this? People are missing! You fuckers are selfish. The Dufresnes are in someone’s trunk right now, with duct tape over their mouths. And they’re hungry. That’s a double whammy. Bush, search party of three, you can eat when you find the Dufresnes.
So after that I naturally looked him up on YouTube, and at that point discovered him to be completely different to what I had imagined:
http://www.youtube.com/watch?v=2491LucLa1g
Gone, try this one:
Picture
A lot of infographics annoy me, but I like the idea of bringing together the data that drives this one so much I don’t mind its shortcomings.
Puzzle – The Two Envelopes
I can’t believe I haven’t put this one in Things before.
In a standard abstract setting with no distracting details, you and another person are presented with two envelopes. One envelope contains some money (but you don’t know how much). The other envelope contains twice as much money. You get to select an envelope, and you get to keep however much money is in it. The other person gets the other envelope. There isn’t anything to go on, so you choose one of the envelopes for arbitrary reasons.
Before you get to open it, you are offered the chance to change your mind, with the following reasoning:
You don’t know how much money is in your chosen envelope, but for the sake of argument let’s say it’s £10. That means you either have the envelope with twice as much money (so the other contains £5) or you don’t (so the other must contain £20). So if you decide to swap, there’s a 50% chance you get that £5, and a 50% chance you end up with the £20. Since you currently have £10, that means there’s a 50% chance of effectively losing £5 and a 50% chance of gaining another £10. Imagine if the universe split into two at the moment you made that decision – one of you loses £5, the other gains £10, so on average you gain (£10 + (-£5) )/2 = £2.50. Since the average gain is positive, clearly that’s a gamble worth taking, and you should definitely swap.
This is of course a strange conclusion. You effectively chose an envelope at random, so how does swapping it improve your odds of getting more money? The paradox is even more stark if we consider the fact that the other person could be convinced to swap by exactly the same argument.
Previous Puzzle – Co-operating with yourself
Last time I asked how well you would get on with yourself.
Xuan said:
They say that people you dislike/hate are likely to be people who’s characteristics are most like yours. People are most critical of what they see in the mirror. My clone better not have the same taste in clothes.
Which reminded me of a problem the sci-fi stories don’t tend to go into – if there’s suddenly two of you, you’re going to need some more clothes, and one of you will probably have to find another job, and probably somewhere else to live. Marriages get complicated. Phil suggested David Gerrold’s time-travel sci fi story The Man Who Folded Himself for an in-depth dissection of this kind of problem.
Richard observed that he tends to like people with whom he shares attractive personality traits, and dislike those that share his negative personality traits, suggesting that the latter may be because they serve as a reminder of these aspects of himself. This potentially makes the question even harder to answer, although one might guess that a negative would trump a positive and ultimately lead to the kind of confrontations that usually crop up in sci-fi versions of this problem (and endorsing Xuan’s observation).
I think the question raised by The Man Who Folded Himself of co-operating with a version of yourself in the future is a clue to how we can actually ask this question of ourselves. In a very real sense, we really do choose how much to co-operate with our future selves every day: will you do a chore now, or will you force your future self to do it instead? Will you eat all of the cake, or will you save some for your future self? If you know how you generally answer those questions, I suggest this gives you an idea of how well you would get on with yourself.
In practical terms, just thinking of these kinds of questions in this framework makes me more likely to co-operate with my future self, which is probably a good thing. Well, I’m glad that my past self thinks that way, anyway.